ZKPs for Proof of Solvency

Technical Tutorials
,
ZKPs for Proof of Solvency https://celo.academy/uploads/default/original/2X/c/cfac49fb000852853a64e5be04689fb3239cc616.png
none 0.0 0
1

Introduction

In the blockchain and cryptocurrency ecosystem, trust and transparency are paramount, especially for exchanges and custodial services managing user funds. Users need assurance that these platforms hold sufficient reserves to meet their liabilities without compromising privacy or exposing sensitive information. The Proof of Solvency Circuit addresses this challenge by leveraging zero-knowledge proofs (zk-SNARKs).

In this tutorial, we will explore the idea of how zkproof can be used to setup proof of solvency systems.

Key Concepts

  1. Assets (Reserves): This is the total amount of funds that the exchange or custodial service holds.
  2. Liabilities: This refers to the obligations or amounts owed to users (e.g., customer deposits).
  3. Commitment Scheme: A cryptographic hash function used to commit to sensitive data (e.g., balances) without revealing them. One common method is using Pedersen Commitments or Merkle Trees.
  4. Zero-Knowledge Proof: The proof will confirm that the total reserves are greater than or equal to the total liabilities without revealing the specific balances of individual accounts.

Prerequisites

To follow this tutorial, you should have:

  • A solid grasp of cryptographic principles, particularly zk-SNARKs.
  • Experience in Solidity and blockchain development.
    You can follow the pathway here to get a good foundation on zkSnarks

How Such Systems Would Work

  • Step 1: Commitment to User Balances: The exchange collects all individual user balances and commits to them using a cryptographic commitment scheme (e.g., Pedersen Commitments or Merkle Trees). The commitment to a user’s balance should not reveal the actual balance but only a hash representing it. The exchange can use a Merkle Tree to efficiently store and prove the sum of user balances.
  • Step 2: Proving the Total Reserves: The total reserves of the exchange are the sum of all individual user balances (and possibly the exchange’s own funds). The zk proof will verify that the total reserves are greater than or equal to the total liabilities (the amount owed to customers).
  • Step 3: Generating the zk-SNARK (or zk-STARK) Proof: The zk circuit will take as input the committed balances of all users, the total reserves, and the total liabilities. The zk proof will confirm that: Total Reserves≥Total Liabilities\text{Total Reserves} \geq \text{Total Liabilities}Total Reserves≥Total Liabilities This proof is computed using a zero-knowledge proof generator, which ensures the exchange can prove the relationship without revealing any individual user balances.
  • Step 4: Verifying the zk Proof: The zk proof can be verified by anyone (e.g., regulators, auditors, or the public) without revealing sensitive information like individual user balances. The verifier only sees the zk proof, which confirms that the reserves are sufficient.
  • Step 5: Optional: Privacy via Merkle Tree: To provide privacy, the user balances can be stored in a Merkle Tree, where each user’s balance is a leaf. The Merkle root can be used as the commitment. The zk proof will allow the exchange to prove that the sum of balances (via Merkle proofs) is enough to cover liabilities, but no individual balance is revealed.

Proof of Solvency Basic Circuit Design

Let’s illustrate a basic circuit design that would be used for zk-SNARK proof generation:

  1. Commitments to User Balances:

  • For each user, a commitment c_i is generated based on their balance b_i: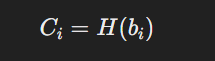

    image

  • This ensures that the balance is hidden, and only the commitment is known.

  1. Total Reserves:

  • The total reserves R are the sum of all user balances: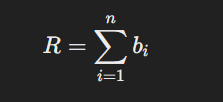

    image

  1. Total Liabilities:
  • The total liabilities L are known and equal to the total amount owed to users.
  1. zk-SNARK Circuit:

  • The zk-SNARK circuit will prove that:
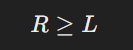
    image

  • The prover inputs the sum of balances (using Merkle proofs or direct commitments), and the circuit checks if the sum of reserves is greater than or equal to the liabilities.

  1. Verification:
  • The verifier can confirm the zk proof, which assures that the reserves are greater than or equal to the liabilities, without revealing any sensitive details (like user balances).

Conclusion

The Proof of Solvency Circuit is a vital tool for enhancing trust and transparency in blockchain-based financial systems. By leveraging zero-knowledge proofs, it allows exchanges and custodial services to demonstrate they hold sufficient reserves to meet their liabilities while safeguarding user privacy. This innovative approach balances the need for accountability with the principles of confidentiality, providing a scalable and secure solution for fostering trust in decentralized and centralized financial ecosystems.

We encourage you to continue your exploration of topics on zk proofs. If you’re interested in diving deeper, you can follow up on the pathway here Zero-Knowledge Proofs on the Celo Blockchain: A Comprehensive Tutorial Series - Pathways - Celo Academy

Resources

Circom docs
SnarkJS
0xparc Circom Workshop
[ZK Learning Group 2] Circom workshop #3 - building an end-to-end zkSNARK app

privacy-scaling-explorations/zkp-app-boilerplate: Build your zkp app with typescript, hardhat, circom, and snarkjs!

Building a Zero Knowledge web app with Halo 2 and Wasm (part 1) | by Yu Jiang Tham | Medium

Building a Zero Knowledge web app with Halo 2 and Wasm (part 2) | by Yu Jiang Tham | Medium

About the author

I’m Jonathan Iheme, A full stack block-chain Developer from Nigeria. With a great passion for Zero Knowledge Technology.

linkedIn
Twitter